Enhancing sample.int for unequal probability sampling

C
R
Wishlist
Models
Author

Ahmadou Dicko and Thomas Lumley

Problem statement

The method of unequal probability sampling without replacement, as implemented in base::sample (base::sample.int), relies on a sequential algorithm (coded in C). This algorithm does not respect the prescribed inclusion probabilities (as defined by the prob parameter). Consequently, it can produce a biased Horvitz-Thompson estimate.

The issue can affect other packages as illustrated by this dplyr issue affecting slice_sample.

To better understand the problem, consider the illustration below, following (Tillé 2023).

set.seed(123)
N <- 12
n <- 4
p <- (1:N)/sum(1:N)
pik <- n * p
pikest_base <- vector(mode = "numeric", length = N)
nsim <- 1e4
for (j in 1:nsim) {
  s <- sample.int(n = N, size = n, replace = FALSE, prob = p)
  pikest_base[s] <- pikest_base[s] + 1
}
pikest_base <- pikest_base/nsim

After estimating the inclusion probabilities with sample.int, we can compare them with algorithms from the sampling package, as highlighted in its documentation.

library(sampling)
set.seed(42)
pikest_maxent <- sapply(1:nsim, \(i) UPmaxentropy(pik))
pikest_maxent <- rowMeans(pikest_maxent)

pikest_pivot <- sapply(1:nsim, \(i) UPpivotal(pik))
pikest_pivot <- rowMeans(pikest_pivot)

cbind(pik,
      pikest_base,
      pikest_maxent,
      pikest_pivot)
             pik pikest_base pikest_maxent pikest_pivot
 [1,] 0.05128205      0.0587        0.0544       0.0511
 [2,] 0.10256410      0.1194        0.1050       0.1049
 [3,] 0.15384615      0.1699        0.1507       0.1486
 [4,] 0.20512821      0.2279        0.2008       0.2058
 [5,] 0.25641026      0.2778        0.2553       0.2538
 [6,] 0.30769231      0.3233        0.3129       0.3149
 [7,] 0.35897436      0.3627        0.3593       0.3556
 [8,] 0.41025641      0.4181        0.4110       0.4111
 [9,] 0.46153846      0.4652        0.4577       0.4607
[10,] 0.51282051      0.4967        0.5115       0.5205
[11,] 0.56410256      0.5189        0.5651       0.5579
[12,] 0.61538462      0.5614        0.6163       0.6151

To evaluate the accuracy of the sampling algorithm, we can compute the following test statistic:

\[ z_k = \dfrac{(\hat{\pi_k} - \pi_k) \sqrt{M}}{\sqrt{\pi_k (1 - \pi_k)}} \]

where \(M\) is the number of simulations.

\(z_k\) should be asymptotically normal under the null hypothesis that the sampling algorithm is correct. The implementation is as follows:

test_stat <- function(est, pik)
  (est - pik) / sqrt(pik * (1 - pik)/nsim)

We can compute this test statistics for each method and check its normality using a qqplot.

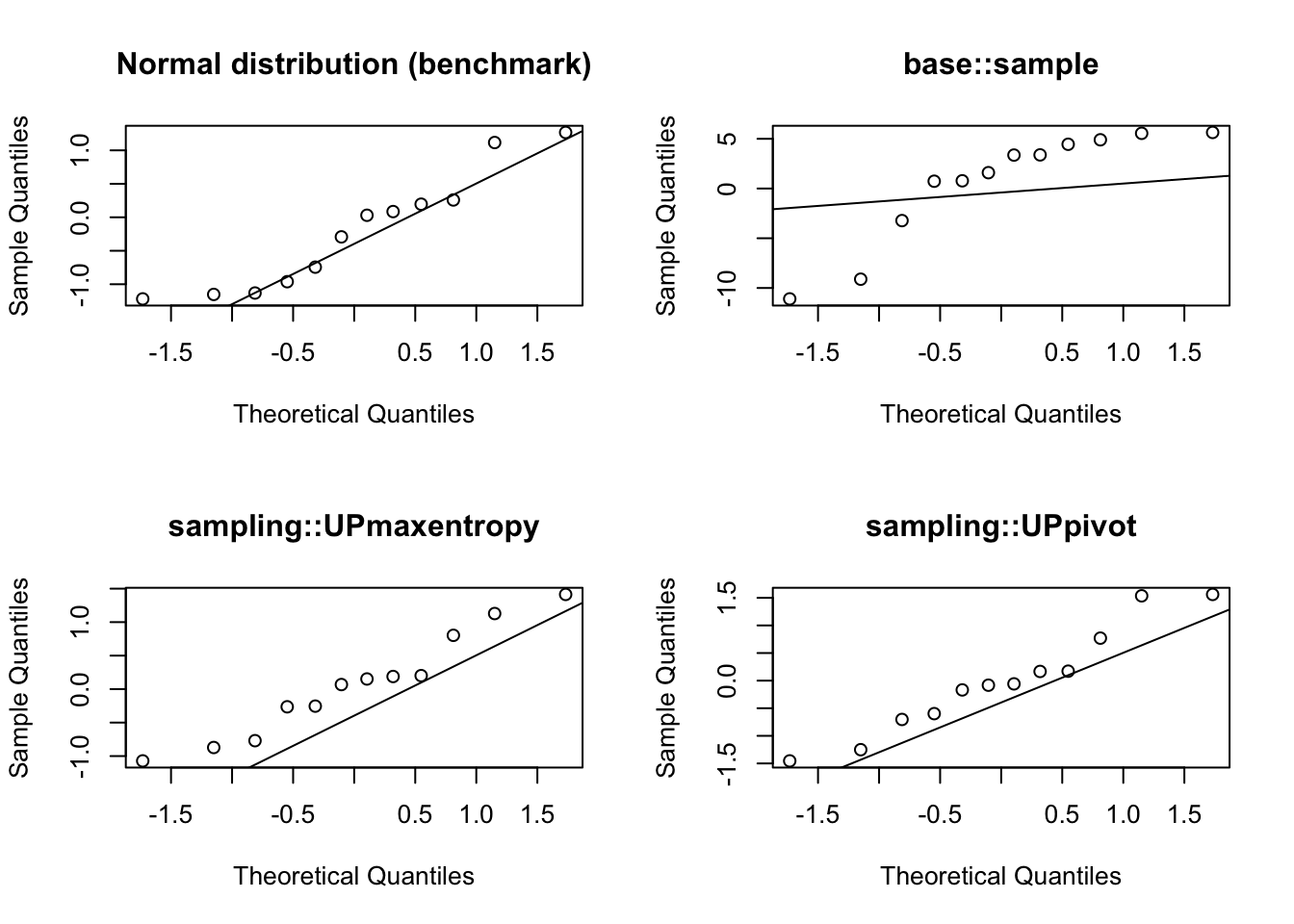
These charts show how base::sample deviates more from normality compared to the other two competing algorithms available in the sampling package.

Proposed solution

  • Option 1:
    • Refine the documentation for base::sample and base::sample.int.
    • Suggest adding a concise paragraph in the Details section, explaining why the function is not suitable for unequal probability sampling based on inclusion probabilities.
  • Option 2:
    • Introduce a new C function and an additional argument to sample.int to incorporate the new method.
    • Retain the original ProbSampleNoReplace C function.
    • By default, base::sample.int should utilize ProbSampleNoReplace for unequal probability sampling without replacement. This ensures backward compatibility and prevents disruptions to existing code.

It is hard to pick one algorithm over the multitude of available unequal probability sampling algorithms. In theory, there’s no best algorithm for unequal probability. However, the Maximum Entropy Sampling algorithm (sampling::UPmaxentropy) also known as Conditional Poisson Sampling is an algorithm with good properties (maximizing entropy) that can be used as a reference.

Project requirements

  • Good understanding of survey sampling algorithms.
  • Good C and R coding skills.

Project outcomes

An enhanced version of sample (sample.int) with a new argument to select the new algorithm for unequal probability sampling.

References

Tillé, Yves. 2023. “Remarks on Some Misconceptions about Unequal Probability Sampling Without Replacement.” Computer Science Review 47: 100533. https://doi.org/10.1016/j.cosrev.2022.100533.

Reactions and comments